Lambda-Calcul

1) Introduction

L'approche informatique du lambda-calcul est plus facilement abordable en proposant directement de la programmation ce qui rend la recherche plus empirique et moins ingrate. Le lambda-calcul peut-être présenté comme le plus petit langage de programmation fonctionnelle possible. Il met en oeuvre deux opérations fondamentales que sont ; la construction d'applications unaires en transformant un élément du calcul en une variable d'entrée, et son application sur un élément, une approche éminemment combinatoire.

Mais nous ne voulons pas développer une science purement combinatoire, nous l'associons tout de suite à une structure algébrique qui lui donne un sens intuitif beaucoup plus riche, sans pour autant restreindre le modèle d'une quelconque façon. On se place dans un ensemble infini `E` en bijection avec l'ensemble des applications définissables de `E` dans `E`. Ainsi tout élément de `E` possède un second rôle, celui d'une application de `E` sur `E`. La transformation de l'élément en la fonction se fait en empruntant la bijection `varphi` dont l'existence est assurée par l'axiome du choix et par la cardinalité l'ensemble des applications définissables. Puis, afin de simplifier les formules, nous ne notons pas l'application `varphi`. On laisse à la syntaxe le soin d'enlever l'ambiguité des rôles des éléments, à savoir quel rôle ils jouent si c'est leur premier rôle d'élément ou leur second rôle d'application. Le modèle ainsi construit n'admet pas d'éléments distincts ayant le même second rôle. C'est le choix d'une application `varphi` injective de `E` vers `E^E` atteignant toutes les applications définissables, qui se traduit par l'axiome d'égalité d'application :

`AAxAAy, (AAz, x(z)"="y(z))⇒x"="y`

On ne va pas tout de suite utiliser le langage minimaliste du lambda-calcul rendant quelque peu hermétique cette matière. Ayant au préalable donné un sens mathématique, une sémantique aux objets évoqués que sont des éléments possédant un second rôle d'application sur eux-mêmes, nous allons au contraire explorer différentes notations et langages transcrivant ces mêmes objects, fidèle à l'adage suivant :

2) L'application sur un élément

Si on utilise cette seule opération qui est l'application d'une application sur un élément, et que l'on pose quelques éléments `{a,b,c}`, on définit le langage alpha engendré par ces éléments, ici en notation habituelle :

`"<" a^"⊙",b^"⊙",c^"⊙" ">" = {a,c,a(b),c(b(a)),a(b)(c),b(a(c)(a))(b)(a)...}`

Cette opération d'appel d'application, lorsqu'elles s'emboitent, possède une priorité syntaxique à gauche d'abord, faisant que `f(x)(y)(z)` désigne l'appication de `f` sur `x` produisant un résultat que l'on applique à son tour sur `y`, produisant un résultat que l'on applique à son tour sur `z`. Dans ce langage, le terme est apellé plus précisement un alpha-terme. On ajoute le shéma d'axiomes de curryfication :

`AAfAAxAAy, f(x,y)=f(x)(y)`
`AAfAAxAAyAAz, f(x,y,z)=f(x)(y)(z)`
`AAfAAxAAyAAzAAt, f(x,y,z,t)=f(x)(y)(z)(t)`
...

Ce shéma d'axiomes définit les fonctions d'arités supérieur à 1. Cela permet d'élargire le langage alpha unaire en un langage alpha multi-aire satisfaisant la curryfication, et donc dans lequel il est possible de faire que le résultat d'une application ne soit jamais réappliqué à un élément `x` puisque l'on peut ajouter tout-de-suite cet élément `x` la fin de la liste des arguments du premier appel.

`f(x)(y)(z)=f(x,y,z)`

Noter que la liste d'arguments fait apparaitre un opérateur virgule qui est associatif et qui correspond à l'opérateur de concaténation de liste, mais qui n'intervient que dans les appels de fonction. Avec cette simplification, on obtient le langage terminologique multi-aire :

`"<" a^"∘",b^"∘",c^"∘" ">" = {a,a(b),c(a(b),b),a(b(a,c)),a(a,b(c,a),c,b(b,b))...}`

On peut noter explicitement l'opération `"⋆"` d'application d'une application sur un élément, avec une syntaxe centrée, on obtient le langage alpha explicite :

`f"⋆"x``=``f(x)`

En cas d'emboitement du même opérateur, la priorité syntaxique est définie à gauche d'abord. Ainsi nous avons :

`f(x)(y)(z)``=``[[f"⋆"x]"⋆"y]"⋆"z`
`f(x)(y)(z)``=``f"⋆"x"⋆"y"⋆"z`

Puis il est possible de noter l'opération `"⋆"` par absence de symbole en juxtaposant les arguments, à condition que les variables soient représentées par des caractères, on obtient le langage alpha réduit :

`f(x)(y)(z)``=``[[fx]y]z`
`f(x)(y)(z)``=``fxyz`

3) Notation

L'appel de fonction à l'anglaise étant une notation habituelle trés répandue chez les néophytes, on réservera les parenthèses `( )` uniquement pour faire des appels de fonction.

Et pour prioriser, on utilisera les crochets `[ ]`. Pour éviter un usage trop intensif des crochets, on priorise les opérateurs comme suit :

• La déclaration de variable à l'aide d'un quantificateur `AA` ou `EE`, définie un bloc dans lequel le langage est augmenté de cette variable, et ce bloc s'étend jusqu'à la fin de la formule ou bien jusqu'à rencontrer un crochet fermant.
• La déclaration de variable à l'aide de l'opérateur `"↣"` ou `"."`, définit un bloc dans lequel le langage est augmenté de cette variable, et ce bloc correspondant à son second argument.
• La virgule est de priorité syntaxique la plus faible juste au dessus de celles des déclarations de variables à l'aide de quantificateur.

4) La composition d'applications unaires

La composition d'applications est associative. C'est une propriété suffisamment importante pour justifier de lui définir un opérateur spécifique noté `"∘"` comme suit. On écrit la définition dans les 3 formes de langage alpha ; traditionnelle, explicite et réduit :

`AAfAAgAAx, [f"∘"g](x) = f(g(x))`

`AAfAAgAAx, [f"∘"g]"⋆"x = f "⋆"[g"⋆"x]`

`AAfAAgAAx, [f"∘"g]x = f [gx]`

 

`AAfAAgAAhAAx, [f"∘"g"∘"h](x) = f(g(h(x)))`

`AAfAAgAAhAAx, [f"∘"g"∘"h]"⋆"x = f "⋆"[g"⋆"[h"⋆"x]]`

`AAfAAgAAhAAx, [f"∘"g"∘"h]x = f [g[hx]]`

5) La construction d'application

La construction d'application consiste à choisir une variable qui va servir de variable d'entrée, pour transformer une expression en une application unaire. Par exemple considérons un alpha-terme `f(a(b))(b)`, si on choisit `b` comme variable que l'on quantifie universellement, on définit l'application `b ↣ f(a(b))(b)`. Le symbole `b` ne désigne plus l'élément `b` dans la fonction, mais la variable libre d'entrée de l'appplication. Ce nouvel opérateur `↣` introduit une quantification universelle sur son premier argument qui doit être une variable. Puis, la portée de cette déclaration de variable se limite à son deuxième argument.

La flèche `|->` désigne un arc. Ainsi un ensemble d'arcs `{a|->b,b|->b,c|->a}` forme un graphe et désigne une fonction qui envoie `a` sur `b`, et qui envoie `b` sur `b`, et qui envoie `c` sur `a`. La flèche `↣` déclare une variable universellement et désigne un ensemble d'arcs :

`b↣f(a(b))(b) = uuu_(b in E){b|->f(a(b))(b)}`

La notation s'étend pour les alpha-termes multi-aires  :

`[a,b]↣f(a(b),b) = uuu_(a in E, b in E){[a,b]|->f(a(b),b)}`

Les variables de l'entête (toutes de noms différents) sont quantifiées universelllement, et ont une portée sur le bloc de code qu'est le deuxième argument définissant le corps de la fonction, et elles masquent les variables de même nom du bloc parent. Le corps de la fonction peut lui même contenir des constructions d'applications tel que par exemple `x↣x(y↣x)`. Cet exemple définit l'application qui prend un élément `x`, qui regarde l'application à laquelle elle correspond, et qui l'applique sur un élément qui est la fonction constante renvoyant toujours `x`.

L'opérateur `↣` possède une syntaxe centrée. La priorité syntaxique est minimal juste au dessus de celle de l'égalité. Son premier argument devant être directement une variable, la priorité syntaxique est nécessairement à droite d'abord. Le premier argument de l'opérateur `"↣"` doit être une variable, et s'il désigne un élément alors il définit une variable de même nom qui va masquer l'élément dans le corps de la fonction. On obtient le lambda-calcul traditionnel :

`f=x"↣"f(x)`
`f=x"↣"y"↣"f(x)(y)``=``x"↣"[y"↣"f(x)(y)]`
`f=x"↣"y"↣"z"↣"f(x)(y)(z)``=``x"↣"[y"↣"[z"↣"f(x)(y)(z)]]`

Remarquez que l'associativité de la composition se transcrit grâce à la currification en une liste d'arguments. On étend le langage pour permettre de noter ces listes de variables de noms différents entre crochets comme premier argument de l'opérateur `"↣"`.

`f=x"↣"y"↣"f(x,y)``=``[x,y]↣f(x,y)`
`f=x"↣"y"↣"z"↣"f(x,y,z)``=``[x,y,z]↣f(x,y,z)`

On définit l'opérateur point "`"."`" comme étant un alias de l'opérateur `↣`. C'est un synonyme. Il possède exactement les mêmes propriétés, seul le nom change. L'opérateur point peut prendre comme premier argument une liste de variables distinctes entre crochet, c'est alors une déclaration de plusieurs variables dont la portée se limite toujours au second membre :

`f=x"."f(x)`
`f=x"."y"."f(x,y)``=``[x,y]"."f(x,y)`
`f=x"."y"."z"."f(x,y,z)``=``[x,y,z]"."f(x,y,z)`

L'opérateur point "`"."`" a une priorité syntaxique minimal juste au dessus de celle de l'égalité, donc plus faible que celle de l'opérateur `↣`, et possède une priorité syntaxique à droite d'abord. On obtient le lambda-calcul explicite :

`f=x"."f"⋆"x`
`f=x"."y"."f"⋆"x"⋆"y``=``[x,y]"."f"⋆"x"⋆"y`
`f=x"."y"."z"."f"⋆"x"⋆"y"⋆"z``=``[x,y,z]"."f"⋆"x"⋆"y"⋆"z`

En notant l'opérateur `"⋆"` par absence de symbole, à condition que les variables soient représentées par des caractères, on obtient le lambda-calcul réduit (sans lambda) :

`f=x"."fx`
`f=x"."y"."fxy``=``[x,y]"."fxy`
`f=x"."y"."z"."fxyz``=``[x,y,z]"."fxyz`

Puis les déclarations successives de variables sont regroupés en utilisant l'opérateur lambda, on obtient le lambda-calcul :

`f=x"."fx=lambdax"."fx`
`f=x"."y"."fxy``=``lambdaxy"."fxy`
`f=x"."y"."z"."fxyz``=``lambdaxyz"."fxyz`

6) Le lambda-calcul

On obtient un langage ne comprenant que deux opérateurs binaires le point "." et l'étoile `"⋆"` avec les crochets de priorisation `[]`. Notez que l'opérateur point "." est une déclaration de variable, et ne doit donc prendre comme premier membre qu'une variable. Et la portée de cette variable ne s'étend pas au delà de son second membre. L'écriture explicite met en exergue les deux opérateurs binaires qui vont servir pour implémenter le lambda-terme, précisant la façon de le mettre en mémoire dans un ordinateur.

L'opérateur point "`"."`" a une priorité syntaxique minimal juste au dessus de celle de l'égalité donc plus faible que celle de l'opérateur `↣`, et possède une priorité syntaxique à droite d'abord.

L'opérateur `"⋆"` s'évalue à gauche d'abord.

Voici la définition de quelques combinateurs de Curry :

7) L'implémentation d'un lambda-terme

Une expression écrite en lambda-calcul s'appelle un lambda-terme. Un emboitement d'applications queclonques s'appelle un alpha-terme. L'alpha-terme est implémenté sous forme d'un arbre qui peut avoir des sous-arbres partagés, autrement dit, c'est un graphe orienté sans cycle. Par exemple :

`f(a(b))(b)``=``[f"⋆"[a"⋆"b]]"⋆"b`

On utilise une structure de données commune qui implémente des graphes orientés avec racine, décrite ici. Les noeuds sont ternaires, la première case indiquant l'opérateur, et les cases suivantes sont les arguments de l'opérateur. Et les feuilles sont identifiées à des éléments mis en étiquette, et il n'y a qu'une feuille pour représenter le même élément.

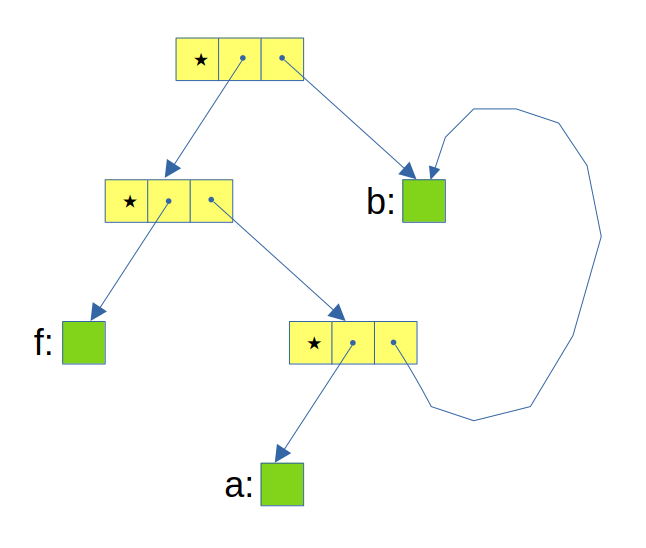
Le lambda-terme est un perfectionnement du alpha-terme. Il introduit des variables quantifiées universellement qui servent d'entrées aux applications. Le nom d'une variable quantifiée universellement, à condition de toujours différer des autres noms de variables présentes dont il doit se distinguer, n'a pas d'importance. Ce sont ses occurences qui déterminent sa signification. C'est pourquoi la façon dont le lambda-terme est implémenté, ne mémorise pas le nom des variables quantifiées universellement. C'est un graphe orienté sans cycle qui mémorise chaque occurences par un partage d'un sommet du graphe. Par exemple :

`b↣f(a(b))(b)`

La variable `b` quantifiée universellement est représentée par un sommet qui n'a pas d'étiquette. Dans un lambda-terme chaque déclaration de variable se fait en utilisant l'opérateur `↣`, et ainsi, à chaque tel opérateur correspond une et une seule case représentant la variable déclarée universellement par cet opérateur.

8) Entrée/sortie

Un langage de programmation fonctionnelle doit comprendre des commandes d'entrées-sortie. Une entrée de haut niveau parmi les plus simples consiste à lire un élément de `E`. On note l'appel de cette procédure par `⎆`. Comme on peut répéter l'opération autant de fois que l'on veut, cela met en oeuvre un flux d'entrée d'éléments de `E`. À chaque évaluation de cet élément, celui-ci retourne l'élément lu suivant sur le flux d'entrée. On étend le lambda-calcul en ajoutant cet élément spécial qui à chaque évaluation ne retourne pas lui-même mais un élément lu dans le flux d'entrée.

Même raisonnement pour concevoir une sortie. Une sortie de haut niveau parmi les plus simples consiste à écrire un élément de `E`. On note l'appel de cette procédure appliqué à un élément quelconque `x`, par `⎇(x)`. Comme on peut répéter l'opération autant de fois que l'on veut, cela met en oeuvre un flux de sortie d'éléments de `E`. À chaque évaluation de `⎇(x)`, l'élément `x` est envoyé dans le flux de sorti, et la fonction retourne `x`.

On perfectionne le mécanisme pour simuler ce que fait une machine de Turing. On conceptualise un ruban constitué d'une succession de cases, où dans chaque case est écrit un élément de `E`. On programme ainsi 4 fonctions :

• Une fonction qui lit un élément et déplace la tête de lecture d'une case à droite,
• Une fonction qui lit un élément et déplace la tête de lecture d'une case à gauche,
• Une fonction qui écrit un élément (son argument) et déplace la tête de lecture d'une case à droite,
• Une fonction qui écrit un élément (son argument) et déplace la tête de lecture d'une case à gauche.

9) L'unification des termes

Considérons un langage terminologique d'opérateurs générateurs par exemple `a, f("."), g(".,.")` :

`L = "<"a,f("."),g(".,.")">"`

Un terme comprenant des variables libres `x,y` désigne l'ensemble des termes que l'on peut construire en remplaçant les variables libres par des termes quelconques. Par exemple le terme `h(g(x,a),g(y,x))` désigne l'ensemble des termes suivants :

`h(g(x,a),g(y,x)) ≡ {g(g(x,a),g(y,x)) "/" x "∈" L "et"  y "∈" L}`

C'est l'ensemble des termes qui lui sont unifiables. L'égalité d'ensemble entre terme contenant des variables libres se note `≡`. Le noms des variables libres n'a pas d'importance, seuls leur occurences dans le terme est important. De tels sorte que si `x` et `y` sont des variables libres c'est à dire des opérateurs ne figurant pas parmi ceux générateurs du langage, alors `f(x)≡f(y)`. Et d'une manière générale, deux termes sont égaux en tant qu'ensemble si et seulement si il existe une bijection entre les variables libres de l'un et les variables libres de l'autre permettant de transformer le terme en l'autre terme. Considérons un second terme avec des noms de variables libres `t,z,v` différentes de ceux du premier terme, tel que par exemple : `g(g(t,z),g(v,f(z)))`. Il désigne également l'ensemble des termes qui lui sont unifiables. On montre alors assez facilement que l'intersection de ces deux ensembles, qui regroupe les termes qui sont à la fois unifiable avec le premier terme et unifiable avec le second terme, sont exactement ceux unifiables avec le résultat de l'unification des deux termes.

`g(g(x,a),g(y,x)) ~~ g(g(t,z),g(v,f(z))) ≡ g(g(f(a),a),g(v,f(a)))`

L'algorithme d'unification, en mémorisant les termes sous forme de graphes orientés sans cycles, s'avère de complexité linéaire, ce qui en fait une opération fondamentale. L'opération d'unification entre deux termes est notée par le symbole `~~`, et est de priorité syntaxique plus forte que celle d'égalité d'ensemble `≡`.

10) L'unification des alpha-termes

Les alpha-termes se ramènent à des termes multi-aires c'est à dire des compositions d'opérateurs ayant un nombre d'arguments variable. L'alpha-terme `f(x)(y)(z)` correspond au terme multi-aire `f(x,y,z)`. C'est même une égalité si on adopte le shéma d'axiomes de curryfication.

La définition des fonctions se faisant par extension, `f"="g <=> AAx, f(x)"="g(x)`, l'égalité `f"="g` peut toujours se remplacer par l'égalité `f(x)"="g(x)` où `x` est une variable libre. Et on peut répéter l'opération plusieurs fois. L'égalité `f"="g` peut être remplacée par l'égalité `f(x)(y)"="g(x)(y)` où `x` et `y` sont des variables libres. Il est donc toujours possible d'ajouter à la fin de l'alpha-terme un appel sur une nouvelle variable libre. L'algorithme d'unification est compléter pour tenir compte de cette possibilité. Ainsi l'unification `f(a) ~~ f(x)(x(a))(b)` correspondra à l'unification `f(a)(y)(z) ~~ f(x)(x(a))(b)` où `y` et `z` sont deux nouvelles variables libres.

En termes multi-aires, l'unification `f(a) ~~ f(x,x(a),b)` correspondra à l'unification `f(a,y,z)~~ f(x,x(a),b)` où `y` et `z` sont des nouvelles variables libres. Autrement dit, on ajoute autant que nécessaire de nouvelles variables libres en fin de liste d'appel afin que lors de l'unification de deux telles listes, elles soient de même taille. Cette nouvelle faculté nous amène à définir la notion de liste de variables libres notée avec une flèche telle que par exemple `vec x`. Avec cette notation, le shéma d'axiomes de curryfication s'écrit en un seul axiome :

`AAfAAxAA vec y, f(x,vecy)=f(x)(vecy)`

Mais attention, dans ce langage étendu les seuls formes de liste d'arguments autorisées sont des listes ne possédant au plus qu'une seule variable liste placée à la fin tel que par exemple `(x,y,z,vec t)`. Si cette règle n'est pas respectée on constatera que l'unification décrite précédement n'est plus de complexité linéaire et perd ainsi son caractère fondamental. C'est pourquoi on garde cette règle syntaxique restrictive dans notre langage.

11) Correspondance entre les lambda-termes et les propositions logiques du premier ordre

Une variable quantifiée universellement est en fait une variable libre. Et une façon de déclarer libre une variable peut consister à la choisir comme variable d'entrée d'une fonction.

`AAx, P(x) " == " x↣P(x)`

Le symbole `"=="` désigne la correspondance entre une proposition logique du premier ordre et un lambda-terme. La priorité syntaxique de cette opérateur `"=="` est plus faible que celles de tous les autres opérateurs et aussi plus faible que celle des déclarations de variables.

Une variable quantifiée existentiellement peut être remplacée (grace à l'axiome du choix) par sa forme de Skolem qui est une fonction s'appliquant à une liste d'arguments que sont les variables quantifiées universellement présente dans son environnement et préexistantes à sa déclaration.

`AAxAAyEEz, P(x,y,z) <=> EEz(".,.")AAxAAy`

`EEz(".,.")AAxAAy, P(x,y,z(x,y)) " == " (x,y)↣P(x,y,z(x,y))`

Où `z` est un élément de `E` qui n'a pas été préalablement défini, et qui correspond donc à la variable `z` déclarée existentiellement. Dans cette forme de Skolem, l'ensemble des fonctions quantifiées existentiellement est placé au début de la formule sous une forme prénexe, de telle sorte qu'il peut être enlevé de la formule pour être ajouté au langage, faisant que la formule redevient une formule logique du premier ordre, mais dans un langage plus riche.