1. Introduction

Les ondes constituent un phénomène auto-entretenu parmi les plus simples à modéliser, et elles constituent la base de l'électromagnétisme. Nous allons explorer ce phénomène en commençant par l'étudier dans un univers unidimensionnel ne possédant qu'un axe du temps. Et on commencera par étudier le signal sinusoïdal.

Puis nous reprendrons notre discussion sur la génèse et sur la nature du signal. Si on conçoit au départ le signal le plus simple, un signal sinusoïdal, celui d'un photon, comment faire naître les équations de Maxwell-Lorentz en partant de ce seul signal ?

La physique s'appuie sur le calcul différentiel pour définir des modèles qui sont des systèmes d'équations différentielles partielles. La nature donne toujours une solution et le modèle peut toujours être choisie comme étant analytique. Aussi, nous n'étudirons le calcul différentiel que pour des fonctions analytiques, des fonctions qui en tout point de leur domaine de définition se développent en série entière convergente sur un voisinage.

Néanmoins, le langage de ces équations peut paraître quelque peu hermétique pour les non-initiés. Et ce n'est pas par la construction de démonstration rigoureuse que l'on fait découvrir la puissance intuitive de ce langage.

Les mathématiques peuvent-être abordées comme la physique. Ce sont toutes deux des sciences hypothético-déductives, et il n'est pas nécessaire d'obtenir la preuve formelle d'une théorie pour l'utiliser si on a la conviction que celle-ci est valide. Ce n'est alors ni plus ni moins qu'une hypothèse. La preuve rigide est ainsi remplacée par l'hypothèse. Et des modèles possédant un formalisme incomplet parceque suceptible de se décliner en plusieurs modèles différents, peuvent jouer ce rôle d'hypothèse. L'expérimentation joue alors le rôle d'élément de preuve, des preuvent incomplètes certes mais qui peuvent, comme en physique, récuser ou conforter le modèle et l'hypothèse ou même les façonner.

On décrira le calcul différentiel des fonctions analytiques à l'aide d'un langage algébrique prometteur obtenue par extension élémentaire, et que l'on confortera par l'expérimentation, ce qui rend la présentation au néophyte beaucoup plus facile. On utilisera les hyperréels et d'autres extensions de structures pour substituer les démonstrations d'analyse par des démonstrations d'algèbre. Mais, aborder ce sujet ainsi sous un autre point de vue paradigmatique ouvre une autre voie qui consiste à refonder l'Analyse, son objet et son but. Voir Analyse et espace métrique

2. Le déterminisme

Tout effet a une cause, et la cause qui constitue également un effet, posséde à son tour une cause, et ainsi de suite. La cause d'une cause est une cause comme les autres, qui possèdent à son tour une cause. La première de toutes les causes qui n'a pas de cause, ou qui est sa popre cause - et qui explique l'existence du monde - n'est pas de ce monde. Elle existe dans un monde tout autre, pas un monde parallèle ou une vague copie du nôtre, non, un monde où il n'y a pas de temps et qu'il ne faudrait pas appeler monde car tellement différent... et où l'entendement est différent et inconnu, où tout est possible. Cela dit, c'est un raccourci théologique facile qui répond à la question existentiel du monde sans vraiment y répondre, à l'image des doctrines religieuses sur la génèse.

En d'autre terme, dans notre monde, le physicien s'attache à révéler le déterminisme des lois du monde, qui constitue son intelligibilité. Et tout ce qui échappe à ce déterminisme est déterminé par des variables extérieures inconnues. Le hasard est donc la manifestation d'intrusion de causes inconnues, et n'existe donc pas en soi. Cette idée et exprimée par Einstein dans l'adage "Dieu ne joue pas aux dès". Restreindre cet idée consiste alors à s'interdire de chercher davantage.... L'obscurantisme est alors de quel coté d'après-vous ?.

Ainsi, les choses étant déterminées, ce qui constitue l'essence de l'intelligibilité du monde, on pourrait pensé que cela n'existe pas, comme tout ce qui est répétition immuable. Mais si !.... Car cela n'a jamais était calculé, jamais était réalisé avant. C'est d'ailleurs cette effectivité première du calcul qui constitue une des composantes paradigmatique du temps.

3. La symétrie du temps

Aussi surprenant que cela puisse paraître, la notion de flèche du temps qui distingue le passé du futur est une notion purement macroscopique. Car à l'échelle microscopique les lois régissant les interactions entre particules respectent une symétrie parfaite selon le sens du temps. C'est à dire que si l'on inverse le sens du temps, en remplaçant dans les équations `t` par `"-"t` et donc `dt` par `"-"dt`, on obtient les mêmes équations, les mêmes lois.

Si on regarde un film à l'envers en remontant le temps, on voit une scène se dérouler dans le sens inverse du temps comme par magie. Une telle scène peut se réaliser, car d'un point de vue microscopique les lois sont respectés, et pourtant cela nous parrait impossible. C'est parceque nous sommes dans une chaine causale dominante définissant cette notion macroscopique qu'est la flêche du temps, une flêche du temps qui n'est qu'apparence et illusion. Rien ne nous interdit d'imaginer l'existence de chaines causales inversées.

Tout étant déterminé, la connaisance de l'univers à un instant donnée détermine aussi bien l'univers future que l'univers passé. La notion de flêche du temps est liée au second principe de la thermodynamique, à la notion de désordre ou d'entropie toujours croissante. Et si on constate une voilation de cette loi, rien ne pourra distinguer cette violation avec l'introduction d'une chaine causale inverse, elle-même soumise à cette loi inverse.

4. Langage formel, intuition et liberté

L'art en la matière consiste à inventer un langage formel adapté au problème, désignant une construction efficiente. Et ce langage deviendra un vecteur incontournable de transmission du savoir. L'enjeux devient alors colossal. Et le principal frein au développement de ce type de recherche reste causé par les nombreux préjugés, dont pour la plus part, nous n'avons pas conscience, qui sont ancrés en nous plus ou moins profondément. Ils agissent comme des oeillères, et nous pouvons difficilement nous en débarrasser dans la vie quotidienne. Ceux qui s'en sont défait ont ainsi acquit un avantage certain pour avancer dans ces études savantes.

Il y a de nombreuses façons de décrire un système déterministe. La notation est importante car elle transporte une intuition, tout un ensemble de non-dits, de mécanismes de reconnaissance, et de règles simples de déduction. Qu'est-ce qui rend si difficile le dévoilement des différents concepts et nous arrête dans notre élan créateur ?. C'est le conformisme et l'absence d'intuition. L'intuition joue un rôle moteur, essentiel dans la génèse des concepts. Il y a donc tout un travail préliminaire pour appréhender un espace, sans préjugé, et pour l'étoffer de sens, d'analogies..., d'une gnose, seul moyen de transmettre cette intuition (aux autres ou à soi-même). Mais qu'est-ce qui différencie l'intuition du préjugé ? C'est le jour et la nuit, l'animé et l'inerte. L'intuition crée. L'intuition est naissance, source de développements potentiels, tout en parcourant quelques grands schémas paradigmatiques, sortes de guide spirituel mais davantage comme un rêve aux mutiples formes mouvantes qui se métamorphose au fur et à mesure qu'il se construit. Le préjugé est au contraire formel, et n'ouvre pas à discution. Il clos la question. Mais de la même façon que la mort est nécessaire à la vie, le préjugé est nécessaire à l'intuition, sans quoi nous partirions dans toutes les directions à la fois et rien ne pourrait être fonder ni construit. Il faut seulement avoir les bons préjugés au bon moment pour enterrer ce qui doit l'être et les bonnes intuitions pour découvrir les voies qui nous intéressent.

Du langage mathématique, un principe paradigmatique fondamental affirme que l'élément peut désigner toute chose, et donc qu'il est toujours possible de reconsidérer comme étant égaux deux éléments initialement distinct. On appelle cela le principe de fusion. Cette étonnante faculté de l'esprit traduit le fait que l'élément puisse désigner toute chose et permet de se libérer des conformismes redoutables liés à la langue. Certes, l'asservissement décrié sur le langage est généralement celui de la censure ou de la réduction, rendant égale l'un et son contraire, rendant l'expression des idées impossibles. Mais son inverse est également un asservissement redoutable, l'illusion que deux choses de noms différents serait intrinsèquement différentes puisque désignées différemment. Le principe de création permet d'agrandire la langue, le principe de fusion permet de réduire la langue, tout deux nous libèrent des emprises de la langue.

5. Notation du physicien

Un premier critère de localité est à prendre en considération qui permet de définir ce que sont les grandeurs classiques. Il n'y a pas que les vitesses s'approchant de la vitesse de la lumière qui peuvent être qualifiées de non-classique, les simples grandeurs aussi. Le cosmos en son entier ou à traver un cycle-monde ne peut pas être considéré comme un système classique, car trop grand, car il possède alors une qualité d'absolu, ce que ne doit pas avoir un système classique. De même, dans l'infiniement petit où la quantification de l'information va jouer un rôle majeur, une localité trop petite sort également du cadre classique. Une distinction devra donc être faite entre les notions de système quantique, de système classique et de système cosmologique. Et nous verrons en quoi ces notions peuvent être reliées entre-elles par un principe de relativité d'échelle.

Un système est caractérisé par des variables d'état, qui décrivent l'état du système. Le modèle est mathématique et ne fait qu'approcher la réalité. Donc il n'est pas judicieux de se tenir à un seul type de modèle sous peine de ne pas pouvoir évoluer et s'approcher davantage de la réalité. C'est pourquoi il peut-être judicieux d'utiliser un type de modèle inachevé, suceptibles de se compléter en de multiples modèles différents, et ainsi avoir un champ d'exploration beaucoup plus large. Le modèle est rendu inachevé en ne retenant dans sa définition que quelques propriétés jugées fondamentales.

Le modèle comprends des variables d'état qui sont dépendantes analytiquement entre elles et qui définissent l'état du système. La définition d'un modèle se présente comme un programme informatique, et nous allons décrire son langage.

Etant donnée des variables d'état `t,x,y`, on crée une nouvelle variable d'état `f` dépendant explicitement des variables `t,x,y` en posant l'existence d'une fonction analytique qui appliquée aux arguments `t,x,y` calcule `f`. On déclare cette existence par le neurone suivant qui joue le rôle de prototype de fonction :

`f ← (t,x,y)`

Le neurone `f"←"(t,x,y)` signifie que la variable d'état `f` est totalement déterminée par les trois variables d'état `(t,x,y)`. On dira que `f` est une variable de sortie ou bien est la tête du neurone, et que les variables `t,x,y` dans cet ordre sont les variables d'entrée ou les racines du neurone.

Si `f` n'est la tête que d'un seul neurone de ce type `RR ← (RR×RR×RR)`, alors le neurone définit sans ambiguïté une fonction de même nom `f(".,.,.")`. Il définie la variable d'état `f` comme étant le résultat de la fonction `f(".,.,.")` portant le même nom, appliquée aux arguments par défaut `(t,x,y)` précisés dans le neurone et qui doivent être des noms de variables d'état.

Ainsi la variable d'état `f` s'apparente à une fonctions analytique `f(".,.,.")` à trois arguments. Le résultat de la fonction est une variable qui porte le même nom que la fonction, c'est le principe de la notation du physicien. Le neurone qui précise cela, précise l'argument par défaut, faisant que dans les formules, là où l'on attend un élément du type de la variable `f`, c'est à dire ici un réel, l'expression `f` désignera `f(t,x,y)`. Le neurone précise ainsi un système de coordonnées `(t,x,y)` par défaut pour la variable `f`.

`f=f(t,x,y)`

Le langage se veut toujours économe en écriture mais devant toujours permettre une adaptation rapide. Rappelons l'adage : "La moitier de la résolution d'un problème s'opère dans le choix d'un langage adapté". Evitons les inutiles précisions lorsqu'il n'y a pas d'ambiguïté. Le typage permet de distinguer des fonctions de même nom lorsqu'ils sont de type différent.

Par exemple si `f` n'est la tête que d'un seul neurone de type `RR"←"RR"×"RR`, alors le neurone définie sans ambiguité une fonction de même nom `f(".,.")`.

`f ← (x,y)`

`f=f(x,y)`

On utilisera ainsi l'inférence de type pour économiser des déclarations superflus dans l'ébauche d'un formalisme toujours en construction. Car rappelez-vous : "Le choix du langage adapté au problème constitue la moitier de sa résolution". Parcontre s'il y a une ambiguïté, il faut alors la lever en précisant de quelle fonction il s'agit, soit en utilisant une forme d'appel spécifique mentionnée dans le neurone, ou soit par un appel avec label. Par exemple considérons le cas où `f` est la tête de plusieurs neurones de même type :

`f ← (x,y)`

`f ← (u,v)`

L'appel `f(".,.")` est alors ambigüe. La nature des fonctions analytiques font que deux fonctions analytiques basées sur un même ensemble de variables racines, et qui sont égales sur un voisinnage, sont nécessairement identiques sur tout le domaines connexe obtenue en étendant ce voisinnage. Ainsi la fonction évoquée est déterminée par l'ensemble des variables racines choisi pour la calculer. On peut donc toujours utiliser un appel avec label précisant l'ensemble des variables choisie (appelés base de variables) pour la calculer.

`f{x"="x,y"="y}`

Dans cet appel avec label, l'ordre des arguments n'a pas d'importance puisqu'ils sont nommés. Les arguments sont des égalités où le premier membre est un nom de variable d'état et le second membre une expression qui servira d'argument.

`f=f{x"="x,y"="y}=f{u"="u,v"="v}`

Puis on autorise une seconde forme de neurone précisant une forme d'appel spécifique. Par exemple :

`f←(x,y)`

`f←[u,v]`

Délors les noms des fonctions associés à leur forme d'appel `f(".,.")` et `f[".,."]` ne sont plus ambigües.

`f=f(x,y)=f[u,v]=f{x"="x,y"="y}=f{u"="u,v"="v}`

Remarquez que l'expression d'un calcul quelconque correspond à une variable d'état anonyme, ou s'il on veut, dont le nom correspond à l'expression de son calcul.

Lorsqu'une déclaration de neurone se fait avec une forme d'appel spécifique déjà existante, la syntaxe autorisée par celle-ci remplace alors la syntaxe autorisée précédente. Cela permet d'adapter la notation par simple redéclaration de neurone avec forme d'appel spécifique. Par contre l'appel avec label est toujours valable en toute circonstance.

6. Les fonctions analytiques

Le domaine de définition d'une fonction analytique est par principe un ensemble ouvert connexe dans un espace métrique. Autrement dit, pour tout point du domaine de définition il existe un rayon non-nul tel que la boule de ce rayon, centrée sur le point en question, soit incluse dans le domaine de définition, et la prolongation par voisinage successif de cette boule redonne le domaine de définition tout entier.

Les fonctions analytiques ont une propriété tout à fait remarquable et qui les définit, c'est qu'elles se développent autour de tout point de leur domaine de définition en une série entière, appelé série de Taylor, convergente sur un voisinnage. Considérons le neurone suivant :

`f"←"(t,x,y)`

La fonction analytique `f(".,.,.")` se développe au voisinage de tout point `(t,x,y)` de son domaine de définition, en une série entière appelée série de Taylor de `f` au voisinage de `(t,x,y)`. Pour formaliser le voisinage, on définit les variables arbitrairement petites `deltat,deltax,deltay`

`f (t"+"deltat,x"+"deltax,y"+"deltay) = sum_(i,j,k) a_("("i,j,k")") deltat^i"·"deltax^j"·"deltay^k`

Les indices `i,j,k` parcours l'ensemble des entiers naturels. Les constante `a_("("i,j,k")")` sont les coefficients de la série entière appelée série de Taylor de `f` au point `(t,x,y)`. Le coefficient `a_("("i,j,k")")` est le produit d'un coefficient multinomiaux et d'une dérivée partielle :

`a_("("i,j,k")") = 1/(i!j!k!) (del^(i"+"j"+"k)f)/(delt^i del x^jdel y^k)`

7) Un exemple

Considérons un système caractérisé par quatres variables d'état réels `u,v,t,x`, et les neurones `(u,v)"←"(t,x)` On a regouper les deux neuronnes ayant les mêmes racines, `u"←"(t,x)` et `v"←"(t,x)`

Considérons que la variable `t` indique le temps, et que la variable `x` indique une position, une position réel sur la droite réel `bbbR`. La variable réel `x` étant une variable d'entrée indépendante du temps, elle constitue ce que l'on appelle un indice réel. À un instant `t`, le système est décrit par les valeurs de `u` et de `v` pour chaque valeur d'indice réel `x`.

La génèse s'accomode mal avec l'infini. Aussi nous prendrons un exemple plus simple où `x` se situe non pas sur la droite des réels `bbbR`, mais sur un cercle, `x "∈" [0,2pi["⟲"`. Et on a pris le radian comme unité puisque cette unité est canonique pour le cercle. On a ajouté le symbole `"⟲"` pour indiquer que l'on referme l'intervalle en reliant la fin au début sans rien modifier d'autre. C'est le même intervalle mais muni d'une structure comprenant une métrique particulière appelé variété différentielle et que nous appellerons variété algébrique en la redéfinissant algébriquement.

A chaque instant `t`, l'état du système est décrit par l'ensemble de triplets suivants, qui correspond au graphe de deux courbes selon `x`, qui sont pour des raisons de quantité d'information finie, nécessairement analytique, et le symbole `⟲` est important car cela précise une propriété analytique des courbes en question : elles doivent être analytiques au voisinnage de `x"="0` qui coïncide au voisinage de `x"="2pi`. L'état du système à l'instant `t` est donc décrit par cet ensemble :

`{(u(t,x),v(t,x),x) "/" x"∈" [0,2pi["⟲"}`

8. De la nature analytique

La Nature tranche toujours toutes les situations en proposant une solution naturelle puisque supposée déterminée..., et cela s'opère sans mettre en oeuvre une quantité d'information infinie comme le montre l'expérimentation en physique quantique. Or notre modèle utilise les nombres réels, une structure mathématique dépassant la réalité. Un nombre réel transporte une quantité d'information infinie, ce que ne contient pas un état réel. Pour remédier à cet obstacle théorique, on commence par se restreindre aux seuls fonctions analytiques, en invoquant toujours l'intelligibilité supposée du monde et sa capacité de pouvoir dévoiler le détaille de toute ses évolutions, en les regardant de suffisamment prés, faisant que chaque transformations physiques mises en oeuvre se fait finalement toujours de manière harmonieuse et sans à-coup à quelque niveau de dérivée que ce soit. Les fonctions utilisées sont toutes des fonctions analytiques c'est à dire indéfiniment dérivables et développables en tout point du domaine de définition en série entière convergente sur un voisinnage de ce point. C'est l'hypothèse que nous sommes naturellement amené à faire.

Délors les variables de sortie sont des fonctions analytiques c'est à dire indéfiniment dérivables et développables en tout point du domaine de défintion en série de Taylor convergente sur un voisinnage. Dans le cas d'une seule variable d'entrée, `f"←"t`, cela se traduit ainsi :

La variable `f` possède à chaque instant `t` une valeur `f(t)` que l'on note simplement `f` puisque qu'elle possède `t` comme argument par défaut. Les variables dérivées successives se notent `f’, f’’, f’’’,...,f^("("n")"),...` Elles sont dépendantes de `t` comme l'est `f`, et donc leur valeur à l'instant `t` se note pareillement simplement par leur nom :

`f=f(t)`
`f’=f’(t)`
`f’’=f’’(t)`
...
`f^("("n")")=f^("("n")")(t)`

Quelque soit `t` dans le domaine de définition de `f(".")`, il existe un rayon `r">"0` de convergence tel que pour tout `h in ]t"-"r,t"+"r[` nous ayons :

`f"←"t`

`f(t"+"h) = f+f’h+(f’’)/2 h^2+(f’’’)/(3!)h^3+ ... + f^("("n")")/(n!)h^n + ...`

Ce qui s'écrit formellement :

`f(t"+"h) = sum_n (f^("("n")"))/(n!) h^n`

Avec les conventions d'écriture suivante, `0! "=" 1` et `f^("("0")") "=" f`. Et pour la somme, vous aurez remarqué l'utilisation d'une variable d'indice, `n`, qui parcourt par défaut l'ensemble des entiers naturels `NN`. Puis la variable dérivée `f’` est définie formellement comme suit :

`f’"←"t`

`f’ = lim_(h->0) (f(t"+"h)-f)/h`

La démonstration du développement de Taylor se fait habituellement par une démonstration d'analyse. On se propose de le faire par une démonstration d'algèbre. Pour cela, il faudra développer un environnement théorique algébrique un peu plus poussé utilisant les hyperréels, remplaçant l'arbitrairement petit par un infiniment petit, remplaçant les équations de voisinages par des équations locales. Mais dans un premier temps, il conviendra de présenter le développement de Taylor limité, sous l'angle mécanique en étudiant la cinématique, une série limitée que l'on obtient de façon canonique en procédant à une succession d'intégrations.

Toute variable totalement dépendante explicitement ou implicitement, est le résultat d'une fonction analytique, et doit donc être indéfiniment dérivables et développables en tout point du domaine de définition en série de Taylor convergente sur un voisinnage. Il en est de même pour les variables d'entrées. Les variables d'entrée étant arbitraires, leur dépendance arbitraire devront être également analytique. Dans la pratique, souvent, la variable d'entrée dépendra d'une variable représentant le temps et sera de dérivée constante et ses dérivées suivantes seront donc nulles.

9. Notation ensembliste

Etant donné un ensemble muni d'une addition `"+"` et d'un produit notée par absence de symbole en juxtaposant les arguments, formant ainsi une structure algébrique. Et étant donnés quelques uns de ses éléments `x,y` et quelques une de ses parties `A,B`.

On adopte la notation ensembliste. Les calculs peuvent combiner des éléments et des ensembles. Et ils s'interprètent en créant des variables existentielles à chaque ensemble :

`x"+"A`	`=`		`{x"+"y "/"EEy "∈" A}`
`A"+"B`	`=`		`{x"+"y "/" EEx "∈" A, EEy "∈" B}`
`xA`	`=`		`{xy "/" EEy "∈" A}`
`AB`	`=`		`{xy "/" EEx "∈" A, EEy "∈" B}`

De même on donne un sense à l'égalité entre un élément et un ensemble qui est le suivant :

`x"="A`	`<=>`		`EEy "∈" A, x"="y `	`<=>`	`x "∈" A`
`x"="y"+"A`	`<=>`		`EEz "∈" A, x"="y"+"z`	`<=>`	`(x-y) "∈" A`

Lorsque `x"="y"+"A` on dit que `x` égale `y` à `A` près.

Si la structure est de plus, munie d'une relation d'ordre stricte `"<"` ou non-stricte `"⩽"`, on adopte la notation ensembliste, faisant que quelque soit un élément `x` de la structure, et quelques soient des parties `A,B` de la structure, la relation entre un élément et un ensemble, ou entre un ensemble et un élément, ou entre deux ensembles, s'interprètent en créant des variables universelle à chaque ensemble :

`x"<"A`	`<=>`		`AAy "∈" A, x"<"y`
`A"<"x`	`<=>`		`AAy "∈" A, y"<"x`
`A"<"B`	`<=>`		`AAx"∈" A, AAy"∈" B, x"<"b`

10. Ordre différentiel

Le calcul différentiel s'intéresse aux petites variations pour établir les lois qui s'opèrent exclusivement localement dans un modèle. Mais une petite variation multipliée par un nombre entier peut toujours devenir une grande variation qui n'est alors plus locale. Pour s'affranchire de cela, il faut rompre avec cet axiome d'archimède, et inventer des nombres infiniments petits, ou dits infinitésimaux, qui sont plus petits que tous les réels strictement positifs, ainsi, multipliés par n'importe quel entier naturel, ils restent toujours infinitésimaux. On passe ainsi de l'infini potentiel que représente le nombre arbitrairement petit, à l'infini acté que représente le nombre infinitésimal `epsilon`.

Ce passage à l'infini acté correspond à une extension élémentaire de corps ordonnée, c'est à dire correspond à l'ajout dans `RR` d'un nouvel élément `omega` plus grand que tous les réels, pour produire encore une structure de corps ordonnée. Une telle extension n'est pas toujours possible. Elle peut aboutire à une incohérence ou à une réduction drastique de la structure résultat. Mais tel n'est pas le cas ici, cela aboutit à une structure des hyperréels, un corps totalement ordonné non-archimédien contenant les réels.

On suppose donc l'existence cohérente de cette structure de corps des hyperréels totalement ordonnée contenant `RR`, engendrée par `RRuu{omega}` où `RR<omega`.

Cela va nous permettre d'enrichir le concept de suite convergente de réels et de manipuler ces suites comme on manipulerait des nombres hyperréels.

Les nombres infinitésimaux sont des hyperréels. Ce sont des nombres infiniment petit vis-à-vis de `1`, et qui apparaissent par le choix d'un étalon de l'infiniment petit noté `epsilon`, marquant le passage de l'infini potentiel à l'infini acté. Cette première génération de nombres infinitésimaux constituent des infiniments petits du premier ordre, c'est à dire de l'ordre de `epsilon`, dont l'ensemble se note `O(epsilon)`. Si on multiplie deux tels éléments, on obtient alors un élément du second ordre, de l'ordre de `epsilon^2` qui est un infiniment petit vis-à-vis de `epsilon`, et dont l'ensemble se note `O(epsilon^2)`. Et ainsi de suite... L'ensemble des nombres réels `RR` fait partie de l'ensemble des hyperréels de l'ordre de `1` qui se note `O(1)` et constitue une strate archimédienne, mais `O(1)` est plus vaste que `epsilonRR` puisqu'il comprend tous les ordres inférieurs ou égaux et leurs sommes finies :

`RR ⊂ O(1)`
`epsilon RR⊂O(epsilon)`
`epsilon^2 RR⊂O(epsilon^2)`

Il apparait symétriquement un étalon de l'infiniment grand `omega =1"/"epsilon`. C'est ainsi que l'on perçoit une partie des hyperréels par le biais d'une suite croissante d'ordres différentiels :

` ... O(epsilon^3) ⊂ O(epsilon^2) ⊂ O(epsilon) ⊂ O(1) ⊂ O(omega) ⊂ O(omega^2) ⊂ O(omega^3) ...`

Les ordres différentiels s'emboitent comme des poupées russes mais ne se mélangent pas : les sommes finies ou convergentes d'éléments d'un ordre produisent un élément du même ordre. Et le produit de deux éléments est dans l'ordre résultant du produit des deux ordres.

Les hyperreéls constituent une extension du corps des réels totalement ordonnés mais non-archimédien. Il est à noter qu'il existe une version dénombrable satisfaisant aux seuls propriétés du premier ordre de la structure. Car c'est une propriété de la logique du premier ordre que de toujours posséder au moins un modèle dénombrable.

Puis les hyperreéls que nous utiliserons seront toujours stratifiés c'est-à-dire appartiendront toujours à :

`"...+"omega^3RR"+"omega^2RR"+"omegaRR"+"RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+..."` 

Le monde des fonctions analytiques est celui des séries entières convergentes en tout points du domaine de définition sur un voisinnage.

Pour toutes fonctions analytiques `f`, et pour tout point `x` de son domaine de défintion, la fonction se développe en une série entière convergente sur un voisinage de ce point `x`. Et cette série entière s'appelle la série de Taylor de `f` en `x`. Prenons par exemple une fonction analytique `f` à une variable `x`, que l'on développe autours de `x`. Pour formaliser un voisinnage de `x` on définit une valeur `h` arbitrairement petite mesurant un éloignement de `x` :

`f"←"x`

`f(x"+"h) =a_0+a_1 h+a_2 h^2+a_3 h^3+...=sum_n a_n h^n`

Le coefficient `a_n` est égale à :

`a_n = (f^("("n")"))/(n!)`

L'extension du corps de réel par l'ajout d'un inifiniment petit `epsilon` va permettre de calculer `f(x"+"epsilon)` en une valeur hyperréelle stratifiée c'est à dire appartenant à `RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+..."` que l'on peut par la suite tronquer à l'ordre que l'on veut. Le remplacement de l'arbitrairment petit `h` par l'infiniment petit `epsilon` nous permet de tronquer la série à un ordre arbitraire, en ajoutant cet ordre à la fin :

`f(x"+"epsilon) = a_0+O(epsilon)`
`f(x"+"epsilon) = a_0+a_1x + O(epsilon^2)`
`f(x"+"epsilon) = a_0+a_1x + a_2x^2 + O(epsilon^3)`
...

Remarquez attentivement que la fonction `f` appliqué à un réel produit un réel :

`x in RR`
`f(x) in RR`

Tandis que l'extension `f(x+epsilon)` est un hyperréel stratifié :

`f(x"+"epsilon) in RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+...`

La variable `f`, constituant une fonction analytique de `x`, possède une tangente. L'introduction de l'infiniment petit `epsilon` produit une définition locale de cette tangente extrèmement simple car, à l'ordre d'`epsilon`, la fonction `f` coïncide avec la tangente. Autrement dit, la fonction `f` est localement linéaire, et le coefficient de linéarité correspond à sa dérivée.

`AAr "∈" RR, f(x+r epsilon)=f+r epsilon f’+o(epsilon)`

Où `o(epsilon)` désigne l'ensemble des hyperréels infiniment petits devant `epsilon`. Comme on se restreint aux seuls hyperréels stratifiés c'est à dire appartenant à `RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+...`, pour tout entier `n` nous avons l'identité suivante :

`o(epsilon^n)=O(epsilon^(n-1))`

Et on choisit d'exprimer le résultat en utilisant le grand `O` ou le petit `o`, en choississant l'expression qui nous parrait la plus simple.

11. Introduction de l'opérateur de différentialisation `d`

Le déterminisme du système suppose que toutes les variables d'état sont dépendantes d'une variable de temps mais qui n'est pas forcement connue. La libre création de nouvelles variables libres semble contredire ce premier principe, car la variable libre est à l'image de cette variable dite temporelle... On résoud cette difficulté en permettant à la variable temporelle d'être un vecteur qui regroupe en faite plusieurs variables réels libres, l'ensemble de toutes les variables libres. On appelle la base de dépendance originelle l'ensemble des variables libres qui déterminent le système.

Le déterminisme du système suppose que toutes ces variables d'état dépendent d'un ensemble de variables libres constituant la base de dépendance originelle mais qui n'est pas forcement connue.

On considère une évolution infinitésimale du système. Le système étant analytique, chaque variable d'état du système va subire une variation infinitésimale. Le système étant déterminé, ces variations infinitésimales constitueront également de nouvelles variables d'état dépendant de la base de dépendance originelle non nécessairement connue.

11.1 Variable libre

Considérons une variable d'état réel `x`. L'élément différentiel `dx` désigne la variation infinitésimale de `x`. Autrement dit, la variable `x` contient un réel appartenant à `RR`, tandis que la variable `dx` contient un infinitésimal du premier ordre c'est-à-dire appartenant à `epsilonRR`. Et il s'agit d'une définition faisant de la différentialisation `dx` une authentique variable d'état, du fait du déterminisme supposé du système. L'élément différentiel `dx` est donc un hypérréel stratifié de l'ordre d'`epsilon`, mais davantage encore il appartient à une seule strate `epsilon RR` :

`dx in epsilon RR ⊂ O(epsilon)`

Si de plus `x` est une variable d'état libre alors `dx` forme une variable d'état infinitésimale du premier ordre également libre. Cette troncature, supprimant de `dx` les composantes d'ordre inférieurs à l'ordre d'`epsilon`, est imposée par la définition de la différentialisation, comme l'est la définition d'`epsilon`. C'est cette définition qui fait que `dx` a les qualités d'une variable d'état appartenant à `epsilonRR`.

`x in RR`
`dx in epsilonRR`

Et donc, puisque `x`, et `dx` sont des variables d'état, leur évolution dans un système déterminé devront constituer des fonctions analytiques.

On décompose le langage, en séparant dans l'expression `du`, l'opérateur de différentialisation `d`, de la variable d'état `u`. Et on précise la priorité syntaxique de cette opérateur. La différentialisation `d` a une priorité syntaxique posée plus élevée que les opérations `"+ - * / ^ ()"`, faisant que `du^2` est égale à `du"*"du` et non à `d(u^2)`, et appliqué plusieurs fois de suite, elle se compose en une puissance `d(d(du))= d^3u`. Ainsi `d^3` est l'opérateur qui différentialise trois fois de suite.

`du"*"du=du^2`

`d(d(du))= d^3u`

Puis le symbole de la multiplication est presque toujours remplacé par une simple juxtaposition des arguments du produit faisant que :

`dududu=d^3u`
`dxdydz=dx"*"dy"*"dz`

L'expression d'un calcul quelconque correspond à une variable d'état anonyme (ou si vous voulez, dont le nom correspond à l'expression de son calcul). Ainsi l'opérateur `d` peut s'appliquer à une expression quelconque interprété comme une variable d'état anonyme, pour former un nouvel élément différentiel sans ambiguité car la différentialisation est exacte et correspond de fait à une nouvelle variable d'état.

11.2 Variable ne dépendant que d'une variable

Considérons le neurone `u"←"t`. La variable `u` constituant une fonction de `t`, elle possède une tangente. Et à l'ordre d'`epsilon`, la fonction `u` coïncide avec sa tangente car la fonction `u` est localement linéaire. Notons le coefficient de linéarité par `a`. Nous avons donc :

`u"←"t`

`AAr "∈" RR, u(t"+"repsilon)=u+repsilona+o(epsilon)`

Puis il est judicieux de notez la variation infinitésimale arbitraire `repsilon` par l'élément différentiel `dt`, puisqu'il s'agit d'une variation de `t`, somme toute, une restriction des libertés du paramètre qui reste seulement soumis au déterminisme du système, et qui n'a donc pas d'effet.

`u(t"+"dt)=u+adt+o(epsilon)`

Le coefficient de linéarité constitue la définition de la dérivée notée `u’"="a`. L'opérateur de différentialisation `d` appliqué à `u` va créer une variable `du` également liée à `t` parce que le système est déterminé, ce qui entraine le neurone implicite `du"←"t` ce qui permet de définir algébriquement la dérivée `u’` par l'égalité d'hyperréels exacte suivante :

`du"←"t`

`u’"←"t`

`u’ = (du)/(dt)`

La fonction `u` est localement linéaire et le coefficient de linéarité correspond à sa dérivée.

`u(t"+"dt)=u+u’dt+o(epsilon)`

Comme `du` et `dt` appartiennent par définition à `epsilonRR`, on en déduit que `du` possède une particularité propre aux éléments différentiels, il est linéaire, proportionnel à `dt`, il satisfait l'égalité d'hyperréels exacte suivante :

`du = u’dt`

Où `u’=du"/"dt` est appelé la différentielle ou la dérivée de `u`. Notez que le sens précis de la différentielle est ici la fonction `r |-> u’ r` tandis que la dérivée est le coefficient `u’`. Notez que `u(t"+"dt) - u` n'est pas égale à `du`, il l'est seulement à `o(epsilon)` près. Car `u(t"+"dt)` est un hyperréel stratifié n'ayant aucune raison d'appartenir à une seule strate.

`u in RR`

`dt in epsilonRR`

`du in epsilonRR`

`u(t"+"dt) in RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+...`

`u(t"+"dt) = u + du + o(epsilon)`

Dans ce cas simple d'une dépendance à un seule variable `t`, la varibale `u` est fonction seulement de `t`, et la dérivée de `u` s'obtient analytiquement et algébriquement comme suit :

`u’=lim_(h->0) (u(t"+"h)-u)/h`

`u’=(du)/(dt)`

Puis, `du` étant fonction de `t` selon le neurone implicite `du"←"t`, l'expression `du(tau)` désigne la valeur de `du` lorsque `t"="tau`. Il faut donc ne jamais ouvrir de parenthèse après un élément différentiel si celui-ci ne correspond pas à un appel de fonction. Pour éviter les confusions avec l'opération de produit, on préfère noter l'appel de fonction de façon explicite `du{t"="tau}`. Et nous avons :

`dt"←"t`
`du"←"t`
`u’"←"t`

`u’(tau) = u’{t"="tau} = (du{t"="tau})/(dt{t"="tau}) =  lim_(h->0) (u(tau"+"h)-u(tau))/h`

Le terme `dt{t"="tau}` désigne la variation infinitésimale du temps à l'instant `tau`. Dans un système déterminé, cette variation infinitésimale est déterminé. Mais la plus part du temps elle est déterminé de façon arbitraire par un libre choix du mathématicien, ce qui caractèrise une variable `dt` dite libre. Le libre choix de `t`, `dt`, `dt^2`, `dt^3`..., `dt^n`... devra néanmoins satisfaire la condition suffisante que `t` doit être une fonction analytique. Mais dans la plus part des cas, on choisie pour une varaible libre `t`, une évolution linéaire ou `dt` est simplement constant.

On définie l'opérateur de dérivée `d"/"dt` qui calcule la dérivée selon `t`, et on se fixe les mêmes règles syntaxiques que pour l'opérateur de différentialisation `d`. Si `u` est lié à `t` ce qui se note par le neurone `u"←"t`, cela entraine les neurones implicites suivants `u"←"t`, `u’"←"t`, `u’’"←"t`,... `u^("("n")")"←"t` et `du"←"t`, `du^2"←"t`, `du^3"←"t`,... `du^n"←"t`. La définition de `du` s'obtient par l'égalité hyperréelle exacte suivante :

`u ← t`

`du = u’dt`

Les dérivées successivent de `u` s'obtiennent par les égalités hyperréelles exactes suivantes  :

`u ← t`

`u’=d/(dt) u = (du)/(dt)`

`u’’=d/(dt) d/(dt) u = (d/(dt))^2 u = (d^2)/(dt^2) u = (d^2u)/(dt^2)`

`u’’’= d/(dt) d/(dt) d/(dt) u = (d/(dt))^3 u = (d^3)/(dt^3) u= (d^3u)/(dt^3)`

`u^("("n")") = (d/(dt))^n u = (d^n)/(dt^n) u= (d^n u)/(dt^n)`

`u"←"t`

`du = u’dt` 

`d^2u = u’’dt^2` 

`d^3u = u’’’dt^3` 

`d^n u = u^("("n")") dt^n` 

11.3 Variable dépendant de deux variables

Considérons le neurone `u"←"(x,y)`. L'opérateur de différentialisation `d` appliqué à `u` va créée une variable `du` également liée à `x,y` parce que le système est déterminé.

La variable `u` constituant une fonction de `(x,y)`, elle possède un plan tangent. Et à l'ordre d'`epsilon`, la fonction `u` coïncide avec le plan tangent, car fonction `u` est localement linéaire. Notons les coefficients de linéarité par `a` et `b` . Nous avons donc :

`u ← (x,y)`

`AA(r_1,r_2) "∈" RR^2, u(x"+"r_1epsilon, y"+"r_2epsilon) = u+r_1epsilon a+ r_2epsilon b + o(epsilon)`

Puis il est judicieux de notez les variations infinitésimales arbitraires `r_1epsilon` et `r_2epsilon` par les éléments différentiel `dx` et `dy`, puisqu'il s'agit d'une variation de `x` et d'une variation de `y`, somme toute, une restriction des libertés des paramètres à ceux de `dx` et `dy` qui restent seulement soumis au déterminisme du système, et qui n'a donc pas d'effet.

`u(x"+"dx, y"+"dy) = u+adx+ bdy+ o(epsilon)`

Comme `du` et `dx` et `dy` appartiennent par définition à `epsilonRR`, on en déduit que `du` possède une particularité propre aux différentiels, il est lié de façon exacte linéairement à `dx`. et `dy`. Autrement dit, nous avons l'égalité d'hyperréels exacte suivante :

`du = adx+ bdy`

Où `a` et `b` sont les coefficients réels de linéarité, et qui ensemble définissant la valeur de la dérivée vectorielle. Pris séparément, ils définissent les dérivées partielles notées comme suit :

`a=(delu)/(delx)`          et        `b=(delu)/(dely)`

La définition de `du` se note par l'égalité hyperréelle exacte suivante :

`du = (delu)/(delx)dx"+"(delu)/(dely)dy`

Mais arrêtons-nous là pour l'instant et étudions d'abord le cas des fonctions analytiques à une seule variable.

12. La différentialisation `d`

Sauf à quelques rares exceptions où cela est mentionné explicitement, on n'utilisera pas de variable nommée autre que réel, faisant qu'une expression différentielle du `n`-ième ordre apparaitra toujours avec `n` opérateurs de différentialisation. Par exemple la valeur `dx^2dyd^2(dzd^2t)` sera du `8`ième ordre c'est à dire appartiendra à `epsilon^8RR`.

Considérons une variable d'état `f` dépendant de la variable d'état `x` ce qui se note par le neurone `f"←"x`. Les liens considérés sont toujours de dépendance totale, ce qui signifie que `f` est le résultat d'une fonction analytique à une variable, `f=f(x)`. On considère alors la dérivée de `f` selon `x` noté `f'` et qui est définie analytiquement et algébriquement comme suit :

`f"←"x`    `f’=lim_(h->0)(f(x"+"h)-f)/h`     `f’=(df)/(dx)`

La première égalité dite analytique correspond à la définition du passage à la limite dans `RR`. La seconde égalité dite algébrique est une égalité d'hyperréels exacte.

L'extension du corps des réels en un corps d'hyperréels s'obtient par l'ajout de l'infiniment petit `epsilon`. La variable `dx` appartient par définition à `epsilonRR` et il en est de même pour la variable `df`. Cette extension du corps des réels va permettre de définir formellement `f(x"+"dx)` en une valeur hyperréelle appartenant à `RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR "..."`, ou bien exprimé sans utiliser `epsilon`, appartenant à `RR"+"dxRR"+"dx^2RR"+"dx^3RR "..."`. Par définition, nous avons :

`f"←"x`    `x ∈ RR`   `f ∈ RR`   `dx ∈ epsilonRR`   `df ∈ epsilonRR`   `f(x"+"epsilon)∈RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR "..."`

Comme les ordres ne se mélangent pas, `f(x"+"epsilon)` est identifé à une série :

`f(x"+"epsilon) = f_0 "+"f_1epsilon"+"f_2epsilon^2 "... +"f_n epsilon^n "..."`  

L'élément `epsilon` pouvant représenter une variation de `x` de l'ordre d'`epsilon`, on spécialise la formule en remplaçant `epsilon` par `dx` :

`f(x"+"dx) = f_0"+"f_1dx"+"f_2dx^2 "... +"f_n dx^n "..."`  

L'analyse nous dit au chapitre 6 que la fonction analytique `f(".")` se développe au voisinage de tout point `x` de son domaine de définition, en une série entière appelée série de Taylor de `f` au voisinage de `x`. Le voisinage de `x` est formalisé par l'élément différentiel `dx` qui est une variable infinitésimale. L'indice `n` parcours l'ensemble des entiers naturels. Les coefficients `f_n` sont les coefficients de la série entière appelée série de Taylor de `f` au point `x`. Le coefficient `f_n` est la dérivée `n`-ième de `f` divisée par factoriel `n` :

`f (x"+"dx) = sum_n f_n dx^n`    avec     `f_n = 1/(n!) (d^n f)/(dx^n)`

`f(x"+"dx) = f"+"f’dx"+"(f’’)/(2!)dx^2"+"(f’’’)/(3!)dx^3 "... +"f^("("n")")/(n!) dx^n "..."`  

`f(x"+"dx) = f"+"(df)/(dx)dx"+"1/(2!)(d^2f)/(dx^2)dx^2"+"1/(3!)(d^3f)/(dx^3)dx^3 "... +"1/(n!)(d^nf)/(dx^n)dx^n "..."`  

Comme nous supposons un sytème déterminé, les différentielles exactes peuvent être considérée comme des variables d'état du système. Nous déduisons :

`f(x"+"dx) = f"+"df"+"(d^2f)/(2!)"+"(d^3f)/(3!) "... +"(d^nf)/(n!) "..."`  

`f(x"+"dx) = (1 "+"d"+"(d^2)/(2!)"+"(d^3)/(3!) "... +"(d^n)/(n!) "...")f`  

On définit ainsi l'opérateur de translation infinitésimale noté `e^d` qui est égale à l'exponentielle de l'opérateur de différentialisation `d` :

`e^d = 1 "+"d"+"(d^2)/(2!)"+"(d^3)/(3!)"...+"(d^n)/(n!)"..."`

Ainsi lorsque `f"←"x` ce qui signifie que `f"="f(x)`, nous avons alors `e^df = f(x"+"dx)`

`f"←"x`   `f = f(x)`   `e^df = f(x"+"dx)`

13. Cinématique

Par commodité, on utilise la notation du "petit o" de Landau. Etant donné un nombre hyperréel `X`, l'ensemble `o(X)` regroupe tous les hyperréelles négligeables devant `X`, c'est à dire tel que multiplié par n'importe quel entier ils ne peuvent pas atteindre `X`. Dans l'ensemble des hyperréelles stratifiés où nous travaillons, `o(epsilon^n) = O(epsilon^(n"+"1))`.

Les élément différentiels d'ordre `n` appartiennent par définition à `epsilon^n RR`. lorsque `f` ne dépend que de la variable `x`, les dérivées successives de `f` selon sa variable `x` sont définies formellement comme suit :

`f"←"x`

`df=f’dx`	`f’ = (df)/dx`	`f’ = (f(x"+"dx)-f)/dx + o(1)`
`d^2f=f’’dx^2`	`f’’ = (d^2f)/dx^2`	`f’’ = (f’(x"+"dx)-f’)/dx + o(1)`
`d^3f=f’’’dx^3`	`f’’’ = (d^3f)/dx^3`	`f’’’ =(f’’(x"+"dx)-f’’)/dx + o(1)`
`d^nf=f^("("n")")dx^n`	`f^("("n")") =(d^(n)f)/dx^(n)`	`f^("("n")") = (f^("("n"-"1")")(x"+"dx)-f^("("n"-"1")"))/dx + o(1)`

Ainsi, l'équation locale peut s'écrire :

`f←x` `f(x"+"dx) = f+df+(d^2f)/(2!)+(d^3f)/(3!) ...`  `f(x"+"dx) = sum_n (d^n f)/(n!)`

`f←x` `f(x"+"dx) = (1+d+(d^2)/(2!)+(d^3)/(3!)...)f` `f(x"+"dx) = (sum_n (d^n)/(n!)) f` `f(x"+"dx) = e^d f`

Considérons une variable d'état `f` dépendant de la variable d'état `x` ce qui se note par le neurone `f"←"x`. Rappelons que la fonction `f` appliquée à un réel, produit un réel, tandis que appliquée à un hyperréel stratifié, elle produira un hypérréel stratifié. Quelque soit la translation `dx` selon l'axe des `x`, cela ne changera pas la valeur réel de `f`, ce qui se note :

`f(x"+"dx)=f+o(1)`   et aussi quelque soit `n`, on a : `f(x"+"ndx)=f+o(1)`

On arrondire à l'ordre des réels en ajoutant `o(1)`. La valeur de `f(x"+"dx)` est un hyperréelle stratifiée c'est à dire appartenant à `RR"+"epsilonRR"+"epsilon^2RR"+"epsilon^3RR"+..."` que l'on peut par la suite tronquer à l'ordre que l'on veut en ajoutant cet ordre dans l'équation. La même remarque s'applique à la variable d'état `df`. Quelque soit la translation `dx` selon l'axe des `x`, cela ne changera pas la valeur epsilon réel de `df`, ce qui se note :

`df(x"+"dx) = df + o(epsilon)`  et aussi quelque soit `n`, on a : `df(x"+"ndx)=f+o(1)`

Mais pour éviter la confusion entre l'appel de fonction `df(x"+"ndx)` et le produit `df*(x"+"ndx)`, on utilisera l'appel de fonction avec label :

`df{x"="x"+"ndx} = df + o(epsilon)`

La translation selon `x` d'une valeur infiniment petit ne change la valeur de `df` que d'une valeur infiniment petite du deuxième ordre. Intéressons-nous maintenant aux différentialisation multiples de `f`  :

`df = f(x"+"dx)-f + o(epsilon)`

`d(df) = df(x"+"dx)-df + o(d(df))`

`d^2f = df(x"+"dx)-df + o(epsilon^2)`

`d^2f = f(x"+"2dx)-f(x"+"dx) - (f(x"+"dx)-f) + o(epsilon^2)`

`d^2f = f(x"+"2dx)-2f(x"+"dx) +f + o(epsilon^2)`

On translate `x` de `"-"dx` pour simplifier l'expression :

`d^2f = f(x"+"dx)- 2f +f(x"-"dx)+ o(epsilon^2)`

`d(d^2f) = df(x"+"dx)- 2df +df(x"-"dx)+ o(d(d^2f))`

`df(x"+"dx) = f(x"+"2dx)-f(x+dx) + o(epsilon)`
`df = f(x"+"dx)-f + o(epsilon)`
`df(x"-"dx) = f(x)-f(x-dx) + o(epsilon)`

`d^3f = (f(x"+"2dx)-f(x"+"dx)) - 2((fx"+"dx)-f) +(f-f (x"-"dx))+ o(epsilon^3)`

`d^3f = f(x"+"2dx) - 3f(x"+"dx) +3f - f(x"-"dx)+ o(epsilon^3)`

`d(d^3f) = df(x"+"2dx) - 3df(x"+"dx) +3df - df(x"-"dx)+ o(epsilon^3)`

`d^4f = df(x"+"2dx) - 3df(x"+"dx) +3df - df(x"-"dx)+ o(epsilon^4)`

`d^4f = (f(x"+"3dx)-f(x"+"2dx)) - 3(f(x"+"2dx)-f(x"+"dx)) + 3(f(x+dx)-f) - (f-f(x"-"dx))+ o(epsilon^4)`

`d^4f = f(x"+"3dx)- 4f(x"+"2dx) + 6f(x"+"dx) - 4f + f(x"-"dx)+ o(epsilon^4)`

On translate `x` de `"-"dx` pour simplifier l'expression :

`d^4f = f(x"+"2dx)- 4f(x"+"dx) + 6f- 4f(x"-"dx) + f(x"-"2dx)+ o(epsilon^4)`

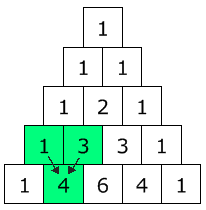
On reconnait dans la disposition des coefficients, le triangle de Pascal.